Generate Keys With Diffie Hellman
Jun 24, 2017 The Diffie-Hellman algorithm is being used to establish a shared secret that can be used for secret communications while exchanging data over a public network using the elliptic curve to generate points and get the secret key using the parameters.
- Generate Keys With Diffie Hellman Music
- Diffie Hellman Group
- Generate Keys With Diffie Hellman Free
- Diffie Hellman Key Exchange Calculator
Create a Diffie-Hellman private key BLOB by calling the CryptExportKey function, passing PRIVATEKEYBLOB in the dwBlobType parameter and the handle to the Diffie-Hellman key in the hKey parameter. When the key handle is no longer needed, call the CryptDestroyKey function to destroy the key handle. After finishing the Diffie-Hellman key exchange, both parties now possess an identical value, known only to each party. This value becomes the 'starting point' from which additional keys can be generated. Earlier, we mentioned Symmetric Encryption and Message Authentication Codes each require a Secret Key.
Definition
Provides a Cryptography Next Generation (CNG) implementation of the Elliptic Curve Diffie-Hellman (ECDH) algorithm. This class is used to perform cryptographic operations.
Generate Keys With Diffie Hellman Music
Examples
The following example shows how to use the ECDiffieHellmanCng class to establish a key exchange and how to use that key to encrypt a message that can be sent over a public channel and decrypted by the receiver.
Remarks
The ECDiffieHellmanCng class enables two parties to exchange private key material even if they are communicating through a public channel. Both parties can calculate the same secret value, which is referred to as the secret agreement in the managed Diffie-Hellman classes. The secret agreement can then be used for a variety of purposes, including as a symmetric key. However, instead of exposing the secret agreement directly, the ECDiffieHellmanCng class does some post-processing on the agreement before providing the value. This post processing is referred to as the key derivation function (KDF); you can select which KDF you want to use and set its parameters through a set of properties on the instance of the Diffie-Hellman object.
| Key derivation function | Properties |
|---|---|
| Hash | HashAlgorithm - The hash algorithm that is used to process the secret agreement. SecretPrepend - An optional byte array to prepend to the secret agreement before hashing it. SecretAppend - An optional byte array to append to the secret agreement before hashing it. |
| Hmac | HashAlgorithm - The hash algorithm that is used to process the secret agreement. SecretPrepend- An optional byte array to prepend to the secret agreement before hashing it. SecretAppend - An optional byte array to append to the secret agreement before hashing it. |
| Tls | Label - The label for key derivation. Seed - The seed for key derivation. |
The result of passing the secret agreement through the key derivation function is a byte array that may be used as key material for your application. The number of bytes of key material generated is dependent on the key derivation function; for example, SHA-256 will generate 256 bits of key material, whereas SHA-512 will generate 512 bits of key material.The basic flow of an ECDH key exchange is as follows:
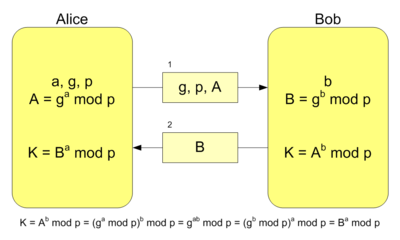
Alice and Bob create a key pair to use for the Diffie-Hellman key exchange operation
Alice and Bob configure the KDF using parameters the agree on.
Alice sends Bob her public key.
Bob sends Alice his public key.
Alice and Bob use each other's public keys to generate the secret agreement, and apply the KDF to the secret agreement to generate key material.
Constructors
| ECDiffieHellmanCng() | Initializes a new instance of the ECDiffieHellmanCng class with a random key pair. |
| ECDiffieHellmanCng(CngKey) | Initializes a new instance of the ECDiffieHellmanCng class by using the specified CngKey object. |
| ECDiffieHellmanCng(ECCurve) | Creates a new instance of the ECDiffieHellmanCng class whose public/private key pair is generated over the specified curve. |
| ECDiffieHellmanCng(Int32) | Initializes a new instance of the ECDiffieHellmanCng class with a random key pair, using the specified key size. |
Fields
| KeySizeValue | Represents the size, in bits, of the key modulus used by the asymmetric algorithm. (Inherited from AsymmetricAlgorithm) |
| LegalKeySizesValue | Specifies the key sizes that are supported by the asymmetric algorithm. (Inherited from AsymmetricAlgorithm) |
Properties
| HashAlgorithm | Gets or sets the hash algorithm to use when generating key material. |
| HmacKey | Gets or sets the Hash-based Message Authentication Code (HMAC) key to use when deriving key material. |
| Key | Specifies the CngKey that is used by the current object for cryptographic operations. |
| KeyDerivationFunction | Gets or sets the key derivation function for the ECDiffieHellmanCng class. |
| KeyExchangeAlgorithm | Gets the name of the key exchange algorithm. (Inherited from ECDiffieHellman) |
| KeySize | Gets or sets the size, in bits, of the key modulus used by the asymmetric algorithm. |
| Label | Gets or sets the label value that is used for key derivation. |
| LegalKeySizes | Gets the key sizes that are supported by the asymmetric algorithm. (Inherited from AsymmetricAlgorithm) |
| PublicKey | Gets the public key that can be used by another ECDiffieHellmanCng object to generate a shared secret agreement. |
| SecretAppend | Gets or sets a value that will be appended to the secret agreement when generating key material. |
| SecretPrepend | Gets or sets a value that will be added to the beginning of the secret agreement when deriving key material. |
| Seed | Gets or sets the seed value that will be used when deriving key material. |
| SignatureAlgorithm | Gets the name of the signature algorithm. (Inherited from ECDiffieHellman) |
| UseSecretAgreementAsHmacKey | Gets a value that indicates whether the secret agreement is used as a Hash-based Message Authentication Code (HMAC) key to derive key material. |
Methods
| Clear() | Releases all resources used by the AsymmetricAlgorithm class. (Inherited from AsymmetricAlgorithm) |
| DeriveKeyFromHash(ECDiffieHellmanPublicKey, HashAlgorithmName) | Performs key derivation using a specified hash algorithm. (Inherited from ECDiffieHellman) |
| DeriveKeyFromHash(ECDiffieHellmanPublicKey, HashAlgorithmName, Byte[], Byte[]) | Performs key derivation using a specified hash algorithm with optional prepended or appended data. |
| DeriveKeyFromHmac(ECDiffieHellmanPublicKey, HashAlgorithmName, Byte[]) | Performs key derivation using a specified HMAC (Hash-based Message Authentication Code) algorithm. (Inherited from ECDiffieHellman) |
| DeriveKeyFromHmac(ECDiffieHellmanPublicKey, HashAlgorithmName, Byte[], Byte[], Byte[]) | Performs key derivation using a specified HMAC (Hash-based Message Authentication Code) algorithm with optional prepended or appended data. |
| DeriveKeyMaterial(CngKey) | Derives the key material that is generated from the secret agreement between two parties, given a CngKey object that contains the second party's public key. |
| DeriveKeyMaterial(ECDiffieHellmanPublicKey) | Derives the key material that is generated from the secret agreement between two parties, given an ECDiffieHellmanPublicKey object that contains the second party's public key. |
| DeriveKeyTls(ECDiffieHellmanPublicKey, Byte[], Byte[]) | Performs key derivation using the TLS (Transport Layer Security) 1.1 PRF (Pseudo-Random Function). |
| DeriveSecretAgreementHandle(CngKey) | Gets a handle to the secret agreement generated between two parties, given a CngKey object that contains the second party's public key. |
| DeriveSecretAgreementHandle(ECDiffieHellmanPublicKey) | Gets a handle to the secret agreement generated between two parties, given an ECDiffieHellmanPublicKey object that contains the second party's public key. |
| Dispose() | Releases all resources used by the current instance of the AsymmetricAlgorithm class. (Inherited from AsymmetricAlgorithm) |
| Dispose(Boolean) | Releases the unmanaged resources used by the AsymmetricAlgorithm class and optionally releases the managed resources. (Inherited from AsymmetricAlgorithm) |
| Equals(Object) | Determines whether the specified object is equal to the current object. (Inherited from Object) |
| ExportECPrivateKey() | Exports the current key in the ECPrivateKey format. (Inherited from ECDiffieHellman) |
| ExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Byte>, PbeParameters) | Exports the current key in the PKCS#8 EncryptedPrivateKeyInfo format with a byte-based password. (Inherited from AsymmetricAlgorithm) |
| ExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Char>, PbeParameters) | /smart-notebook-11-product-key-generator.html. Exports the current key in the PKCS#8 EncryptedPrivateKeyInfo format with a char-based password. (Inherited from AsymmetricAlgorithm) |
| ExportExplicitParameters(Boolean) | Exports the key and explicit curve parameters used by the ECCurve object into an ECParameters object. |
| ExportParameters(Boolean) | Exports the key used by the ECCurve object into an ECParameters object. |
| ExportPkcs8PrivateKey() | Exports the current key in the PKCS#8 PrivateKeyInfo format. (Inherited from AsymmetricAlgorithm) |
| ExportSubjectPublicKeyInfo() | Exports the public-key portion of the current key in the X.509 SubjectPublicKeyInfo format. (Inherited from AsymmetricAlgorithm) |
| FromXmlString(String) | This method is not implemented. |
| FromXmlString(String, ECKeyXmlFormat) | Deserializes the key information from an XML string by using the specified format. |
| GenerateKey(ECCurve) | Generates a new ephemeral public/private key pair for the specified curve. |
| GetHashCode() | Serves as the default hash function. (Inherited from Object) |
| GetType() | Gets the Type of the current instance. (Inherited from Object) |
| ImportECPrivateKey(ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from an ECPrivateKey structure, replacing the keys for this object. (Inherited from ECDiffieHellman) |
| ImportEncryptedPkcs8PrivateKey(ReadOnlySpan<Byte>, ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from a PKCS#8 EncryptedPrivateKeyInfo structure after decrypting with a byte-based password, replacing the keys for this object. (Inherited from ECDiffieHellman) |
| ImportEncryptedPkcs8PrivateKey(ReadOnlySpan<Char>, ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from a PKCS#8 EncryptedPrivateKeyInfo structure after decrypting with a char-based password, replacing the keys for this object. (Inherited from ECDiffieHellman) |
| ImportParameters(ECParameters) | Imports the specified parameters for an ECCurve object as a key into the current instance. |
| ImportPkcs8PrivateKey(ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from a PKCS#8 PrivateKeyInfo structure after decryption, replacing the keys for this object. Acupuncture practice management software mac. (Inherited from ECDiffieHellman) |
| ImportSubjectPublicKeyInfo(ReadOnlySpan<Byte>, Int32) | Imports the public key from an X.509 SubjectPublicKeyInfo structure after decryption, replacing the keys for this object. (Inherited from ECDiffieHellman) |
| MemberwiseClone() | Creates a shallow copy of the current Object. (Inherited from Object) |
| ToString() | Returns a string that represents the current object. (Inherited from Object) |
| ToXmlString(Boolean) | This method is not implemented. |
| ToXmlString(ECKeyXmlFormat) | Serializes the key information to an XML string by using the specified format. |
| TryExportECPrivateKey(Span<Byte>, Int32) | Attempts to export the current key in the ECPrivateKey format into a provided buffer. (Inherited from ECDiffieHellman) |
| TryExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Byte>, PbeParameters, Span<Byte>, Int32) | Attempts to export the current key in the PKCS#8 EncryptedPrivateKeyInfo format into a provided buffer, using a byte-based password. (Inherited from ECDiffieHellman) |
| TryExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Char>, PbeParameters, Span<Byte>, Int32) | Attempts to export the current key in the PKCS#8 EncryptedPrivateKeyInfo format into a provided buffer, using a char-based password. (Inherited from ECDiffieHellman) |
| TryExportPkcs8PrivateKey(Span<Byte>, Int32) | Attempts to export the current key in the PKCS#8 PrivateKeyInfo format into a provided buffer. (Inherited from ECDiffieHellman) |
| TryExportSubjectPublicKeyInfo(Span<Byte>, Int32) | Attempts to export the current key in the X.509 SubjectPublicKeyInfo format into a provided buffer. (Inherited from ECDiffieHellman) |
Explicit Interface Implementations
| IDisposable.Dispose() | For a description of this member, see Dispose(). (Inherited from AsymmetricAlgorithm) |
Applies to
-->Generating Diffie-Hellman Keys
Diffie Hellman Group
To generate a Diffie-Hellman key, perform the following steps:
Call the CryptAcquireContext function to get a handle to the Microsoft Diffie-Hellman Cryptographic Provider.
Generate the new key. There are two ways to accomplish this—by having CryptoAPI generate all new values for G, P, and X or by using existing values for G and P, and generating a new value for X.
To generate the key by generating all new values
- Call the CryptGenKey function, passing either CALG_DH_SF (store and forward) or CALG_DH_EPHEM (ephemeral) in the Algid parameter. The key will be generated using new, random values for G and P, a newly calculated value for X, and its handle will be returned in the phKey parameter.
- The new key is now ready for use. The values of G and P must be sent to the recipient along with the key (or sent by some other method) when doing a key exchange.
Windows 7 home premium activation key generator. To generate the key by using predefined values for G and P
- Call CryptGenKey passing either CALG_DH_SF (store and forward) or CALG_DH_EPHEM (ephemeral) in the Algid parameter and CRYPT_PREGEN for the dwFlags parameter. A key handle will be generated and returned in the phKey parameter.
- Initialize a CRYPT_DATA_BLOB structure with the pbData member set to the P value. The BLOB contains no header information and the pbData member is in little-endian format.
- The value of P is set by calling the CryptSetKeyParam function, passing the key handle retrieved in step a in the hKey parameter, the KP_P flag in the dwParam parameter, and a pointer to the structure that contains the value of P in the pbData parameter.
- Initialize a CRYPT_DATA_BLOB structure with the pbData member set to the G value. The BLOB contains no header information and the pbData member is in little-endian format.
- The value of G is set by calling the CryptSetKeyParam function, passing the key handle retrieved in step a in the hKey parameter, the KP_G flag in the dwParam parameter, and a pointer to the structure that contains the value of G in the pbData parameter.
- The value of X is generated by calling the CryptSetKeyParam function, passing the key handle retrieved in step a in the hKey parameter, the KP_X flag in the dwParam parameter, and NULL in the pbData parameter.
- If all the function calls succeeded, the Diffie-Hellman public key is ready for use.
When the key is no longer needed, destroy it by passing the key handle to the CryptDestroyKey function.
Generate Keys With Diffie Hellman Free
If CALG_DH_SF was specified in the previous procedures, the key values are persisted to storage with each call to CryptSetKeyParam. The G and P values can then be retrieved by using the CryptGetKeyParam function. Some CSPs may have hard-coded G and P values. In this case a NTE_FIXEDPARAMETER error will be returned if CryptSetKeyParam is called with KP_G or KP_P specified in the dwParam parameter. If CryptDestroyKey is called, the handle to the key is destroyed, but the key values are retained in the CSP. However, if CALG_DH_EPHEM was specified, the handle to the key is destroyed, and all values are cleared from the CSP.
Exchanging Diffie-Hellman Keys
The purpose of the Diffie-Hellman algorithm is to make it possible for two or more parties to create and share an identical, secret session key by sharing information over a network that is not secure. The information that gets shared over the network is in the form of a couple of constant values and a Diffie-Hellman public key. The process used by two key-exchange parties is as follows:
- Both parties agree to the Diffie-Hellman parameters which are a prime number (P) and a generator number (G).
- Party 1 sends its Diffie-Hellman public key to party 2.
- Party 2 computes the secret session key by using the information contained in its private key and party 1's public key.
- Party 2 sends its Diffie-Hellman public key to party 1.
- Party 1 computes the secret session key by using the information contained in its private key and party 2's public key.
- Both parties now have the same session key, which can be used for encrypting and decrypting data. The steps necessary for this are shown in the following procedure.
To prepare a Diffie-Hellman public key for transmission
- Call the CryptAcquireContext function to get a handle to the Microsoft Diffie-Hellman Cryptographic Provider.
- Create a Diffie-Hellman key by calling the CryptGenKey function to create a new key, or by calling the CryptGetUserKey function to retrieve an existing key.
- Get the size needed to hold the Diffie-Hellman key BLOB by calling the CryptExportKey, passing NULL for the pbData parameter. The required size will be returned in pdwDataLen.
- Allocate memory for the key BLOB.
- Create a Diffie-Hellman public key BLOB by calling the CryptExportKey function, passing PUBLICKEYBLOB in the dwBlobType parameter and the handle to the Diffie-Hellman key in the hKey parameter. This function call causes the calculation of the public key value, (G^X) mod P.
- If all the preceding function calls were successful, the Diffie-Hellman public key BLOB is now ready to be encoded and transmitted.
To import a Diffie-Hellman public key and calculate the secret session key
- Call the CryptAcquireContext function to get a handle to the Microsoft Diffie-Hellman Cryptographic Provider.
- Create a Diffie-Hellman key by calling the CryptGenKey function to create a new key, or by calling the CryptGetUserKey function to retrieve an existing key.
- To import the Diffie-Hellman public key into the CSP, call the CryptImportKey function, passing a pointer to the public key BLOB in the pbData parameter, the length of the BLOB in the dwDataLen parameter, and the handle to the Diffie-Hellman key in the hPubKey parameter. This causes the calculation, (Y^X) mod P, to be performed, thus creating the shared, secret key and completing the key exchange. This function call returns a handle to the new, secret, session key in the hKey parameter.
- At this point, the imported Diffie-Hellman is of type CALG_AGREEDKEY_ANY. Before the key can be used, it must be converted into a session key type. This is accomplished by calling the CryptSetKeyParam function with dwParam set to KP_ALGID and with pbData set to a pointer to a ALG_ID value that represents a session key, such as CALG_RC4. The key must be converted before using the shared key in the CryptEncrypt or CryptDecrypt function. Calls made to either of these functions prior to converting the key type will fail.
- The secret session key is now ready to be used for encryption or decryption.
- When the key is no longer needed, destroy the key handle by calling the CryptDestroyKey function.
Diffie Hellman Key Exchange Calculator
Exporting a Diffie-Hellman Private Key
To export a Diffie-Hellman private key, perform the following steps:
- Call the CryptAcquireContext function to get a handle to the Microsoft Diffie-Hellman Cryptographic Provider.
- Create a Diffie-Hellman key by calling the CryptGenKey function to create a new key, or by calling the CryptGetUserKey function to retrieve an existing key.
- Create a Diffie-Hellman private key BLOB by calling the CryptExportKey function, passing PRIVATEKEYBLOB in the dwBlobType parameter and the handle to the Diffie-Hellman key in the hKey parameter.
- When the key handle is no longer needed, call the CryptDestroyKey function to destroy the key handle.
Example Code
The following example shows how to create, export, import, and use a Diffie-Hellman key to perform a key exchange.